arXiv: 2305.09929 Slides: kangbo.dev/tdc_slides/index.html
An unambiguous and robust formulation for Wannier localization
Kangbo Li & Anil Damle
Department of Computer Science, Cornell University
Joint work with Hsin-Yu Ko & Robert A. DiStasio Jr.
Department of Chemistry and Chemical Biology, Cornell University
Iterative Localization
Constrained minimization of the sum of the spread (omitting $\mathbf{k}$)
$$ \begin{aligned} \min_{U}\; \Omega(U), \quad \text{s.t. } U^{\dagger} U = I. \end{aligned} $$ A commonly used type of spread is $$ \Omega(U) = \sum_n \bra{\phi_n} \mathbf{r}^2 \ket{\phi_n} - |\underbrace{\bra{\phi_n} \mathbf{r} \ket{\phi_n}}_{\text{orbital center}}|^2 $$$\ket{\phi_{n}} = \sum_{m} U_{nm} \ket{\psi_m}$
Iterative Localization
- Local minimums.
- Need initial guesses.
- Hard to converge.
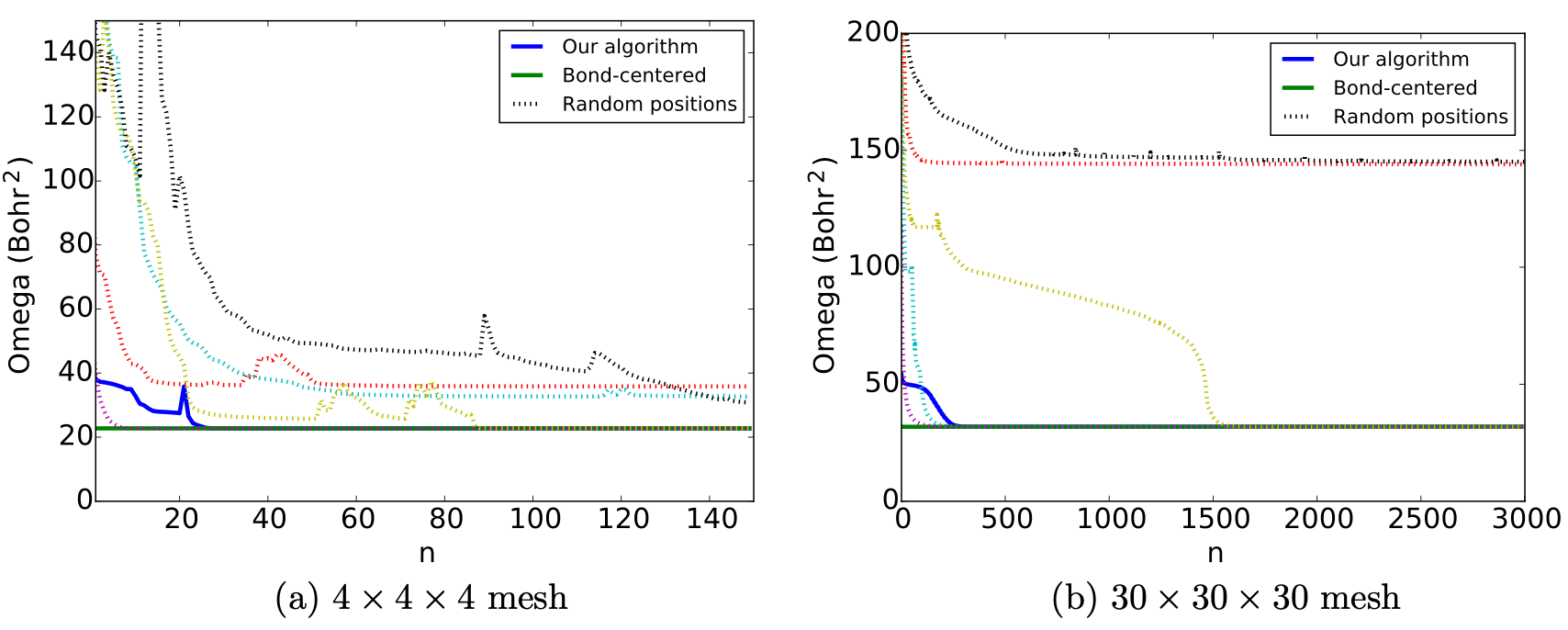
Figure from Cancès, Levitt, Panati, and Stoltz, 2017.
Iterative Localization
Alternative Approaches (incomplete list)
- Projection (Mustafa et.al. 2015): projecting an optimized set of priors.
- SCDM (Damle, Lin, & Ying 2015): CPQR on $\Psi^{T}$.
- Homotopy (Cancès et. al. 2017): parallel transport.
- IPP (Stubbs & Watson 2021): Eigen decomposition.
Iterative Localization
The orbital center is gauge-discontinuous, regardless of how it is defined.
- The center is, naively, just $\bra{\psi} \mathbf{r} \ket{\psi} = \int \mathrm{d} \mathbf{r} \rho(\mathbf{r}) \mathbf{r}$.
- This is ill-defined under PBCs. Resta (1998) suggested $\mathrm{Im} \log z$.
- This formula is computable, but is still gauge-discontinuous.
Any definition of the center should move with the density $$ \mathrm{center}(\mathcal{T}_{\mathbf{y}}\rho) = \mathrm{center}(\rho) + \mathbf{y}. $$ This is inherently incompatible with gauge-continuity under PBCs.
Sidestep the Problem: Variational Formulation
The center of a distribution under open boundary conditions can be defined as "the point around which the distribution has the least second moment."
$$ \begin{aligned} \mathbf{c}^* & \triangleq \argmin_{\mathbf{r}'} \int \rho(\mathbf{r}) (\mathbf{r} - \mathbf{r}')^2 \mathrm{d} \mathbf{r} = \int \rho(\mathbf{r}) \mathbf{r} \mathrm{d} \mathbf{r} \\ s & \triangleq \min_{\mathbf{r}'} \int \rho(\mathbf{r}) (\mathbf{r} - \mathbf{r}')^2 \mathrm{d} \mathbf{r} = \int \rho(\mathbf{r}) (\mathbf{r} - \mathbf{c})^2 \mathrm{d} \mathbf{r} \end{aligned} $$Sidestep the Problem: Variational Formulation
The Density Convolution (DC)
$$ (\mathcal{S} \rho)(\mathbf{r}') = \int \rho(\mathbf{r}) (\mathbf{r} - \mathbf{r}')^2 \mathrm{d} \mathbf{r} $$Open boundary condition
Periodic boundary condition
Sidestep the Problem: Variational Formulation
The Density Convolution (DC)
The center & spread can be derived from the density convolved with $\mathbf{r}^2$ $$ \begin{aligned} (\mathcal{S} \rho) (\mathbf{r}') & \triangleq \int_{{\color{#547bc9} \mathbb{S}_{\mathbf{r}'}}} \rho(\mathbf{r}) (\mathbf{r} - \mathbf{r}')^2 \mathrm{d} \mathbf{r} = \int_{{\color{#547bc9} \mathbb{S}_{\mathbf{0}}}} \rho(\mathbf{r} + \mathbf{r}') \mathbf{r}^2 \mathrm{d} \mathbf{r}. \end{aligned} $$- $\mathbf{c}_{\mathrm{DC}}$ is multivalued and can be gauge-discontinuous.
- $s_{\mathrm{DC}}$ is always well-defined and gauge-continuous.
- $s_{\mathrm{DC}}$ is an unambiguous and computable ground truth.
Sidestep the Problem: Variational Formulation
The Truncated Density Convolution (TDC)
$s_{\mathrm{DC}}$ is global in $k$-space, but we can spectrally approximate it with something local in $k$-space. The result is not new.
$$ \begin{aligned} s_{\mathrm{DC}} & {\color{#a44b69} \gtrapprox } s_{\mathrm{TDC}} \triangleq \sum_{\mathbf{b}} 2 w_{\mathbf{b}} (1 - |\hat{\rho}(\mathbf{b})|),\\ \hat{\rho}(\mathbf{b}) &= \frac{1}{N} \sum_{\mathbf{k}} M_{n,n}^{\mathbf{k}, \mathbf{k} + \mathbf{b}}, M_{n,n}^{\mathbf{k}, \mathbf{k} + \mathbf{b}} = \langle u_{n, \mathbf{k}} | u_{n, \mathbf{k} + \mathbf{b}} \rangle \end{aligned} $$A formal lower bound!
- Large $s_{\mathrm{TDC}}$ $\Rightarrow$ delocalized orbitals.
- Large $s_{\mathrm{MV}}$ $ {\color{#a44b69}\not\Rightarrow}$ delocalized orbitals!
- Shows up consistently in practice.
Sidestep the Problem: Variational Formulation
The Truncated Density Convolution (TDC)
- Has appeared in Berghold et.al. (2000) adapted from Resta (1998).
- Used by Stengel & Spaldin (2006) and Thygesen et. al. (2006).
- Considered "equivalent" to MV (Marzari et. al. 2012).
- There has not been a connection to DC.
Rapid Convergence
Our code (TDC) vs. Wannier90 (MV)
- 50 random initial guage.
- 10x-70x fewer iterations.
- Our code uses a robust stopping criteria.
- $P_c$ is not at $100\%$.
Rapid Convergence
- TDC exhibits fast and monotonic convergence.
- The equivalent local orbitals are reached with either TDC or MV.
- Large $s_{\mathrm{MV}}$ $\not\Rightarrow$ delocalized orbitals.
- $s_{\mathrm{TDC}}$ is a lower bound to $s_{\mathrm{DC}}$.
Take-home
- The center is inherently gauge-discontinuous under PBCs.
- Our formalism is gauge-continuous and appears to resolve the convergence issues.
-
We give a formal bound $s_{\mathrm{TDC}} \leq s_{\mathrm{DC}}$
- Large $s_{\mathrm{TDC}}$ $\Rightarrow$ delocalized orbitals.
- Large $s_{\mathrm{MV}}$ $\not\Rightarrow$ delocalized orbitals.
Software Packages
WTP.jl: Infrastructure code for grids and orbitals
SCDM.jl: Our in-house code for localization.
arXiv: 2305.09929 Slides:kangbo.dev/tdc_slides/index.html
Software Packages
WTP.jl
It allows you to directly write in electronic structure notations.
sum(k->u[n, k]' * u[n, k+b], brillouin_zone)
This does what you expect $\sum_{\mathbf{k}} \langle u_{n, k} | u_{n, \mathbf{k}+\mathbf{b}}\rangle$.
(Before) Future Work
Gradient $\cong$ Suffering
$\Rightarrow$ Automatic differentiation of functionals.
Goals
- Automatic (complex) functional differentiation. ✓
- Symbolic simplification including symmetries. ✓*
- Support second quantization. 𐄂
Help needed with development and PL modeling of second quantization.